Locality diagrams of conformal models

In what follows, we list known locality diagrams associated to conformal models (see 1 and 2 for background), ordered by increasing number of vertices. The pictures represent the reduced locality diagrams, i.e. with the universal vertex (corresponding to the equilocality class of the vacuum) left out; note that the universal vertex is never essential but always self-adjacent. Vertices with a double boundary are the loopy vertices, i.e. those adjacent to themselves, while those filled red are the essential ones (whose omission would change the associated lattice), i.e. the red subgraph is the radical of the diagram. Each diagram is preceded by a conventional alphanumeric label (generated automatically by the classification algorithm) written in bold, and a list of conformal models having the corresponding locality diagram, with the following labeling conventions (when not stated explicitly otherwise, n and k denote arbitrary positive integers, while p,q and r stand for odd primes):

Xk
n with X=A,B,C,D,E,F or G denotes the affine WZNW model of level k based on the simple Lie-algebra Xn of rank n;

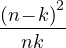Vir(n,k) with coprime integers n and k, denotes the minimal Virasoro model of central charge c=1-6(n- k)2 --nk---;
AT(n) denotes the Ashkin-Teller model with n+7 primaries (the ℤ2-orbifold of the free boson compactified on a circle

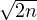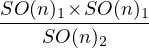of radius R=√ --- 2n), i.e. the coset SO-(n)1×SO-(n)1 SO (n)2;

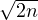G(n) denotes the Gaussian model with 2n primaries (the free boson compactified on a circle of radius R = √ --- 2n), i.e.

the U(1) WZNW model at level n;


SVir1(n) denotes the minimal N =1 superconformal model of central charge c = 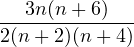--3n(n+-6)--- 2(n + 2)(n + 4), i.e. the

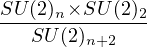SU-(2)n-×SU-(2)2- SU (2)n+2 coset model;

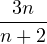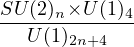
SVir2(n) denotes the minimal N=2 superconformal model of central charge c= -3n-- n + 2, i.e. the SU-(2)n-×U-(1)4 U(1)2n+4

coset model;


PF(n) denotes the parafermionic model of central charge c= 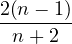2(n---1) n+ 2, i.e. the 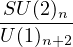-SU-(2)n U (1)n+2 coset;
D(G) denotes the holomorphic orbifold with twist group G (trivial cocycle), with ℤn, 𝔻n, 𝕊n, 𝔸n and Mn denoting

respectively the cyclic, dihedral, symmetric, alternating and Mathieu groups of degree n;


T, O and I denote the isolated c= 1 models, i.e. the orbifolds of SU(2)1 with tetrahedral, octahedral and

icosahedral respective twist groups.


Diagrams


The following table summarizes some of the characteristics of locality diagrams, ordered by increasing number of vertices. The first column gives the conventional label of the diagram, the second the total number Υ of vertices, the third the number ϵ of essential ones, the fourth the size 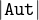|Aut| of the automorphism group (when known), the fifth the number ρ of loops (self-adjacent vertices), the sixth the size λ of the associated lattice, the seventh the dimension δ (length of a maximal chain) of the latter, and finally, the eighth lists some conformal models with the given locality diagram.

label 		Υ ϵ |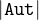Aut| ρ λ δ examples
58A
2
1
1
1
2
1
G(1), A 1
1, A 1
2, A 1
4, A 1
6, E 1
6, E 1
7,
E n+2
8 (n<5), F n
4 (n<9), G n
2 (n<9)
1A
3
2
1
2
3
2
 D(M11), PF(2), A 2
1, A 1
3, A 1
8, B 1
n,
C 1
2, D 1
2n+3, E 2
8, G(2), Vir(4,3)
59A 4 2 2 1 4 2 PF(p), A 2n+1
1, A 3n∓1
2, G(p)
9A 4 3 1 2 4 3 AT(1), A 2n
1, A 3
2, C 1
2n+2, G(4)
62A 4 3 6 4 5 2 D(ℤ2), D 1
4n (n ≤ 3)
62B 4 3 2 2 5 2 D 1
4n+2 (n ≤ 3)
84A 5 4 1 3 5 4 D(𝕊5), D(𝕊6), D(M10), B 2
4, G(8)
76A 5 4 4 3 6 2 D(ℤ3)
76B 5 4 8 1 6 2
2A
6
3
1
2
6
3
 PF(p2), A 2n+1
3, A 2
8, A 4
8, D 3
5, D 3
7, D 3
9, E 2
7
G(2p), G(p2), SVir2(1), SVir1(3)~ =Vir(5,4)
11A 6 4 2 2 6 4 PF(4),AT(p), A 2
3, A 3
8, D 2
5, D 2
7, D 2
11, D 2
13
61A 6 5 1 3 6 5 A 4
3, D 4
5, G(16), T
186A 6 5 2 2 8 3
82A 7 6 4 4 8 4 D(𝕊3)
93A 7 6 16 3 8 2 D(ℤ5)
93B 7 6 48 1 8 2
172A 7 6 1 4 7 6 G(32)
71A 8 3 6 1 8 3 PF(15), A 5
5, A 7
5, G(pq)
63A 8 4 6 4 10 3 D 3
4, D 5
4, D 3
8
63B 8 4 2 2 10 3 D 3
6, D 3
10
3A
8
4
1
2
8
4
 A 2
5, A 3
5, A 4
5, A 8
5, A 5
7, Vir(n+5,n+4),
PF(2p), G(4p), G(p3), PF(27)
90A 8 5 2 4 8 5 A 6
5
15A 8 5 1 3 8 5 PF(8),AT(p2), A 2
7, D 2
9
118A 8 7 12 5 9 4 D(𝔸4)
91A 8 6 2 3 8 6 A 4
7
12A 8 7 6 4 10 5 AT(4), D 2
4, D 4
4, D 6
4, D 4
6, D 4
8
174A 8 7 1 4 8 7 G(64)
187A 8 7 6 2 10 3
83A 9 7 6 6 9 6 D(𝕊4)
10A 9 8 4 4 13 4 AT(2)
95A 9 8 96 3 10 2 D(ℤ7)
95B 9 8 384 1 10 2
14A 9 8 6 5 11 6 AT(8), D 2
8
170A 9 4 2 4 9 4 G(2p2)
180A 9 8 1 5 9 8 G(128)
184A 9 8 16 4 10 4 D(𝔻5)
17A 10 5 6 2 10 5 AT(pq)
21A 10 6 1 3 10 6 AT(27), PF(16)
171A 10 5 1 3 10 5 G(8p)
92A 10 9 16 8 15 4 D(ℤ4)
92B 10 9 48 4 15 4
92C 10 9 8 4 15 4
92D 10 9 8 6 15 4
13A 10 7 2 4 12 5 AT(2p), D 2
6, D 2
10, SVir1(4)
18A 10 9 6 5 12 7 AT(16)
192A 10 9 1 5 10 9 G(28)
23A 11 10 6 6 13 8 AT(32)
193A 11 10 1 6 11 10
190A 11 10 12 2 14 4
190B 11 10 12 4 14 4
185A 11 10 96 4 12 4 D(𝔻7)
5A
12
4
2
2
12
4
 G(p2q), G(2pq), SVir2(p-2) for p > 3,
SVir1(2n+1)
70A 12 5 2 2 12 5 PF(12)
72A 12 5 1 4 12 5 PF(18), G(4p2), G(2p3)
31A 12 7 1 4 12 7 AT(81), PF(32)
16A 12 8 2 4 14 6 AT(4p), D 2
12
29A 12 11 6 6 14 9 AT(64)
4A 12 11 2 4 18 5 SVir2(2)
173A 12 6 1 3 12 6 G(16p)
188A 12 11 120 2 14 3
19A 13 8 2 6 15 6 AT(2p2)
99A 13 12 7680 3 14 2 D(ℤ11)
165A 13 12 7 15 10 AT(128)
25A 14 6 2 3 14 6 AT(p2q)
121A 14 8 1 4 14 8 AT(243), PF(64)
169A 14 8 2 4 16 6 SVir1(2n+2)
20A 14 9 2 5 16 7 AT(8p)
89A 14 12 144 9 16 8 D(M9)
176A 14 7 4 14 7 G(32p)
101A 15 14 - 3 16 2 D(ℤ13)
108A 15 14 - 4 16 4 D(𝔻11)
175A 15 6 6 15 6 G(8p2), G(2p4)
77A 16 15 16 67 4 D(𝔻2)
124A 16 5 2 16 5 PF(30), G(4pq), G(135)
73A 16 6 3 16 6 PF(24)
22A 16 8 4 18 6 AT(2pq)
24A 16 9 6 18 7 AT(4p2)
26A 16 10 5 18 8 AT(16p)
27A 16 9 6 18 7 AT(54)
122A 16 9 5 16 9 AT(36)
177A 16 4 1 16 4 G(105)
178A 16 6 4 16 6 G(108)
110A 17 16 4 18 4 D(𝔻13)
97A 17 16 96 7 23 4 D(ℤ9)
8A 18 5 4 18 5 G(2p2q), SVir2(2p2)
162A 18 6 2 18 6 AT(105)
168A 18 6 4 18 6 PF(36)
181A 18 7 6 18 7 G(144)
33A 18 11 6 20 9 AT(96)

 



Comments

  1. There is only one non-planar (reduced) diagram with less than 11 vertices - the one labelled 18A -, while for a larger number of vertices planar diagrams are the exception.

  2. Many of the diagrams - e.g., those of all Gaussian and parafermionic models - are extremal, i.e. they saturate the fundamental inequality δ ≤ ϵ< Υ ≤ λ in the sense that δ=ϵ and Υ=λ.

  3. Apart from a couple of degenerate cases, the structure of diagrams for unitary minimal Virasoro and N=1 superconformal models follows a simple pattern: there is just one generic Virasoro diagram (3A), while there are two generic N=1 superconformal diagrams (5A and 169A) depending on wether n is odd or even. For other classes of models, the pattern is more complicated, e.g. for N=2 superconformal and Ashkin-Teller models it depends on the prime factorization of the parameter n.