s így a korrelációs függvény:
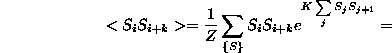
Az állapotösszeget a 15.13 feladatban számítottuk ki:
Bevezetve a
A
Felhasználva, hogy ![]() lehetséges értékei
lehetséges értékei ![]() , írhatjuk, hogy
, írhatjuk, hogy
![]()
s így a korrelációs függvény:
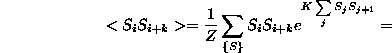
![]()
Az állapotösszeget a 15.13 feladatban számítottuk ki:
![]()
Bevezetve a ![]() jelölést:
jelölést:
![]()
![]()
A ![]() összegzés eredményeként csak akkor kapunk nem
nullát, ha a spinváltozók vagy a nulladik, vagy pedig a masodik hatványon fordulnak elő . Ahhoz, hogy itt az
összegzés eredményeként csak akkor kapunk nem
nullát, ha a spinváltozók vagy a nulladik, vagy pedig a masodik hatványon fordulnak elő . Ahhoz, hogy itt az ![]() és
és
![]() változók négyzete álljon, az kell, hogy a
kitevőt sorbafejtve, a sor valamelyik tagjában szerepeljen
változók négyzete álljon, az kell, hogy a
kitevőt sorbafejtve, a sor valamelyik tagjában szerepeljen ![]() és
és ![]() is. Mivel minden
is. Mivel minden ![]() -vel együtt
-vel együtt ![]() is
megjelenik, az
is
megjelenik, az ![]() és
és ![]() közötti összes spin negyzete kell, hogy szerepeljen. Ilyen tag csak egy van, és ez a kovetkező :
közötti összes spin negyzete kell, hogy szerepeljen. Ilyen tag csak egy van, és ez a kovetkező :
![]()
Ezt a tagot ![]() -re összegezve, az összeg
-re összegezve, az összeg ![]() , tehát
, tehát
![]()
A szuszceptibilitást a 15.18 feladat alapján szamíthatjuk ki:
![]()
![]()
Az utolsó egyenlőség csak termodinamikai határátmenetben
![]() igaz. egyébként ehhez az eredményhez
igaz. egyébként ehhez az eredményhez
![]() nagyságrendű korrekciók adódnak.
nagyságrendű korrekciók adódnak.
Kiegészítés a 15.19 feladathoz