amelynek az
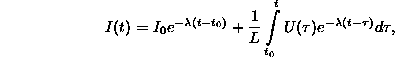
ahol bevezettük a
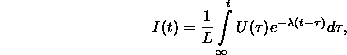
s így
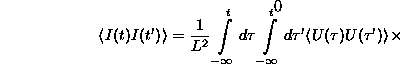
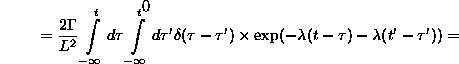
Az áramingadozásokat leíró egyenlet: ![]()
amelynek az ![]() kezdeti feltételt kielégítő megoldása:
kezdeti feltételt kielégítő megoldása: 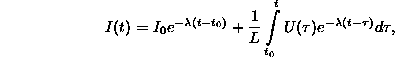
ahol bevezettük a ![]() jelölést. Amennyiben
jelölést. Amennyiben ![]() és
és ![]() , az
, az ![]() korrelációs
függvény nem függ a kezdeti feltételtől, elvégezhető a
korrelációs
függvény nem függ a kezdeti feltételtől, elvégezhető a
![]() határátmenet, és ott az
határátmenet, és ott az ![]() határfeltételt szabhatjuk ki. Ekkor
határfeltételt szabhatjuk ki. Ekkor 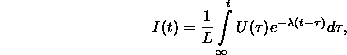
s így 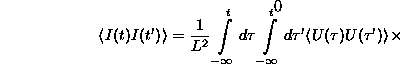
![]()
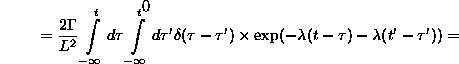
![]()
A ![]() együtthatót abból a feltételből számíthatjuk
ki, hogy az egyidejű korrelációs függvény az áram
egyensúlyi fluktuációit írja le. Erről viszont az ekvipartíció tétele alapján tudjuk, hogy
együtthatót abból a feltételből számíthatjuk
ki, hogy az egyidejű korrelációs függvény az áram
egyensúlyi fluktuációit írja le. Erről viszont az ekvipartíció tétele alapján tudjuk, hogy ![]()
Így tehát
![]()
Ez az eredmény alakilag megegyezik a Brown-mozgást végző\ részecske sebességkorrelációs függvényével. Ennek így is kell lennie, hiszen a kiinduló egyenlet és zaj tulajdonságai mindkét esetben ugyanazok.