tehát
Az
így a rendszer hőmérséklete:
Látható, hogy csak E<0 esetén lehet normális termodinamikai viselkedésről beszélni, mivel E>0 esetén (M>0) a hőmérséklet negatív.
Az (2) egyenletből meghatározható ![]() , s ezzel a betöltési számok
, s ezzel a betöltési számok ![]() és
és ![]() hőmérsékletfüggése:
hőmérsékletfüggése:
![]()
Tehát kanonikus eloszlást kaptunk.
A hőkapacitás meghatározásához először E(T)-t számítjuk ki.
![]()
amelynek T szerinti deriválásából a fajhő :
![]()
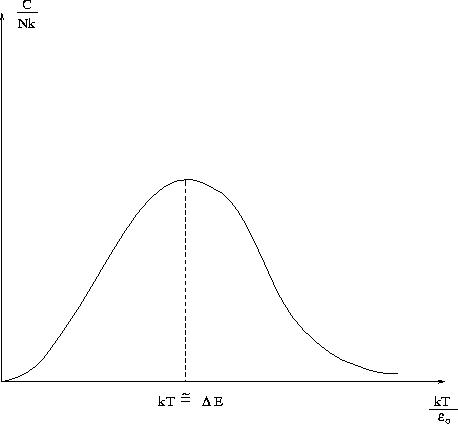
ahol ![]() a gerjesztés energiája. Ez az ún. Schottky-féle fajhő , amelynek jellegzetes maximuma
gyakran megfigyelhető alacsony hőmérsékleten olyan rendszerekben, amelyekben a második gerjesztett
állapot már nem játszik szerepet (
a gerjesztés energiája. Ez az ún. Schottky-féle fajhő , amelynek jellegzetes maximuma
gyakran megfigyelhető alacsony hőmérsékleten olyan rendszerekben, amelyekben a második gerjesztett
állapot már nem játszik szerepet (![]() ).
).