ahol az exponenciális tényező a levágó faktor, a fázistérfogat pedig M gyorsan növekvő függvénye (nagy N esetén
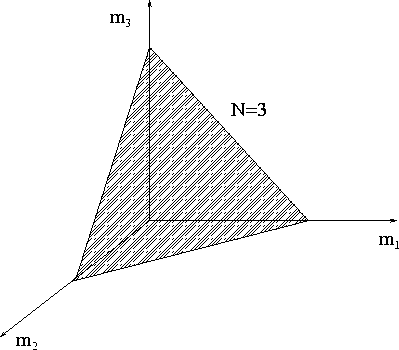
Mikrokanonikus eloszlás esetén a ![]() feltételek által meghatározott síkon
kell átlagolni. A kanonikus eloszlásra való áttérés
azt jelenti, hogy feladjuk a ``tömegmegmaradást'', és a
tes
feltételek által meghatározott síkon
kell átlagolni. A kanonikus eloszlásra való áttérés
azt jelenti, hogy feladjuk a ``tömegmegmaradást'', és a
tes ![]() térrészre átlagolunk, de egy olyan
eloszlással, amelynek
térrészre átlagolunk, de egy olyan
eloszlással, amelynek ![]() függvényében a fent leírt síkon van éles
maximuma (vagyis M átlagos tömegű gyémántokat
vizsgálunk). Az eloszlásfü ggvényt az ideális gáz
mintájára választjuk (ott a
függvényében a fent leírt síkon van éles
maximuma (vagyis M átlagos tömegű gyémántokat
vizsgálunk). Az eloszlásfü ggvényt az ideális gáz
mintájára választjuk (ott a ![]() volt az a feltétel, amit feladtunk):
volt az a feltétel, amit feladtunk): ![]()
ahol az exponenciális tényező a levágó faktor, a
fázistérfogat pedig M gyorsan növekvő függvénye
(nagy N esetén ![]() M
M![]() M). Az exponenciális tényezőben
M). Az exponenciális tényezőben
szereplő ![]() paramétert úgy választjuk meg, hogy a
két tényező szorzatának a maximuma egybeessen az
paramétert úgy választjuk meg, hogy a
két tényező szorzatának a maximuma egybeessen az ![]() -vel meghatározott hipersíkkal. Ezt
úgy érhetjük el, hogy
-vel meghatározott hipersíkkal. Ezt
úgy érhetjük el, hogy ![]() -t a
-t a ![]()
feltételből határozzuk meg. Az ![]() átlag integrálással meghatározható:
átlag integrálással meghatározható: 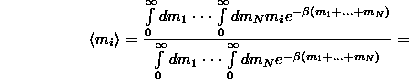
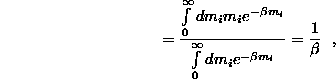
tehát ![]()
s ekkor ![]()
Látszik, hogy ez az eredmény
csak ![]() -ben
különbözik a mikrokanonikus eloszlásból kapott
eredménytől, tehát nagy N esetén a két módszer
azonos eredményre vezet.
-ben
különbözik a mikrokanonikus eloszlásból kapott
eredménytől, tehát nagy N esetén a két módszer
azonos eredményre vezet.