Következő: A 16.25 feladat megoldása
Fel: megoldások
Előző A 16.23 feladat megoldása
A kolloidrészecske mozgásegyenlete

ahol 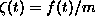 , és
, és 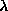 a viszkozitással
arányos tényező. Bevezetve a
a viszkozitással
arányos tényező. Bevezetve a
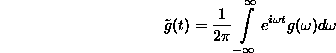
Fourier-transzformációt, a mozgásegyenlet algebrai egyenletté
redukálódik:
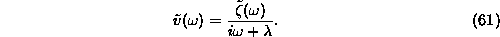
Mivel a 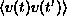 korrelációs függvény csak (t
- t')-től függ, a Fourier-komponensekre vonatkozó
összefüggés a következő alakba írható:
korrelációs függvény csak (t
- t')-től függ, a Fourier-komponensekre vonatkozó
összefüggés a következő alakba írható:
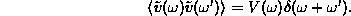
Hasonlóan, a zaj korrelációja
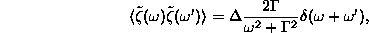
ahol felhasználtuk, hogy az 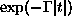 függvény
Fourier-transzformáltja
függvény
Fourier-transzformáltja 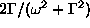 . Ezek
után az (61) egyenlet mindkét oldalát
. Ezek
után az (61) egyenlet mindkét oldalát 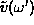 -vel beszorozva, majd átlagolva a zajra,
-vel beszorozva, majd átlagolva a zajra, 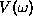 -ra a
következő kifejezés adódik:
-ra a
következő kifejezés adódik:
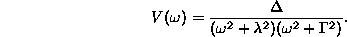
Így a sebességkorrelációs függvény
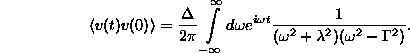
A fenti integrált a reziduumtétel segítségével
számíthatjuk ki. Ha t > 0, akkor a Re 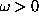 félsíkon
zárjuk be az integrált, és az
félsíkon
zárjuk be az integrált, és az 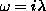 és
és 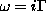 pólusok járulékait adjuk össze, míg t < 0
esetén a Re
pólusok járulékait adjuk össze, míg t < 0
esetén a Re 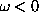 félsíkon levő
félsíkon levő 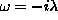 és
és 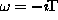 pólusok járulékát kell összeadni. Az
erdmény:
pólusok járulékát kell összeadni. Az
erdmény:
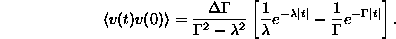
 -t úgy kell megválasztanunk, hogy az ekvipartíció
tétele teljesüljön:
-t úgy kell megválasztanunk, hogy az ekvipartíció
tétele teljesüljön:
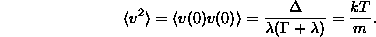
Így tehát
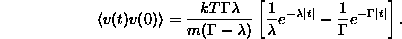
Természetesen a 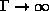 határesetben
visszakapjuk a szokásos Brown-mozgás eredményét.
határesetben
visszakapjuk a szokásos Brown-mozgás eredményét.
16.24 feladat